Neural networks are powerful machine learning models that can learn from data and perform various tasks, such as image recognition, natural language processing, and speech synthesis. However, most neural networks are trained on fixed datasets and cannot adapt to new data inputs that change over time. This limits their applicability to real-world scenarios that involve dynamic and unpredictable data streams, such as medical diagnosis and autonomous driving. To overcome this challenge, researchers have developed a new type of neural network that learns on the job, not just during its training phase. These flexible algorithms, dubbed “liquid” networks, change their underlying equations to continuously adapt to new data inputs [1].
Liquid Neural Networks
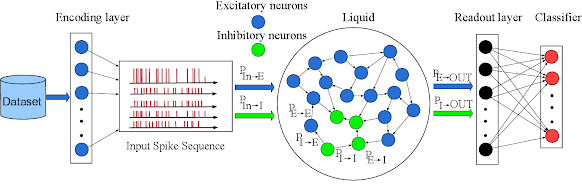
Liquid neural networks are inspired by the nervous system of a microscopic worm called C. elegans, which has only 302 neurons but can generate complex behaviors [1]. Liquid neural networks are composed of linear first-order dynamical systems modulated via nonlinear interlinked gates [2]. They can handle variable-length inputs and enhance the task-understanding capabilities of neural networks [3]. Unlike conventional neural networks, which have fixed weights and activation functions, liquid neural networks have adaptive weights and activation functions that change according to the input data. This allows them to learn from sequential data without forgetting previous information or overfitting to specific patterns [2].
Architecture of Liquid Neural Networks
Liquid Neural Networks (LNNs) are a type of neural network that processes data sequentially and adapts to changing data in real-time, much like the human brain. Unlike traditional neural networks, LNNs can handle variable-length inputs and can change the number of neurons and connections per layer based on new inputs. This allows LNNs to enhance task-understanding capabilities and process continuous or time series data more effectively.
The architecture of LNNs is inspired by the microscopic nematode C.elegans, a 1 mm long worm with a complex nervous system that allows it to perform complex tasks. LNNs mimic the interlinked electrical connections or impulses of the worm to predict network behavior over time, expressing the system state at any given moment.
LNNs have two key features: dynamic architecture and continual learning & adaptability. Dynamic architecture means that LNNs have more expressive neurons than traditional neural networks, making them more interpretable. Continual learning & adaptability means that LNNs can adapt to changing data even after training, mimicking the brain of living organisms more accurately compared to traditional NNs.
LNNs have several advantages over traditional neural networks. They don't require vast amounts of labeled training data to generate accurate results. They have smaller model size and lesser computations, making them scalable at the enterprise level. They are also more resilient towards noise and disturbance in the input signal.
Overall, Liquid Neural Networks offer a promising approach to neural networking that can handle complex, real-time data processing and adaptation, making them a valuable tool for a variety of applications.
Major Use Cases of Liquid Neural Networks
Liquid Neural Networks (LNNs) are a type of neural network that is particularly well-suited for certain types of data processing and analysis. Here are three examples of areas where LNNs have been found to be particularly effective:
- 1. Time Series Data Processing & Forecasting: Time series data is a type of data that is ordered in time, such as stock prices or weather data. LNNs are designed to handle the unique challenges of time series data, such as temporal dependencies and non-stationarity. Researchers have found that LNNs are effective at processing and predicting time series data, and they have been used in applications such as financial forecasting and climate modeling.
- 2. Image & Video Processing: LNNs can be used for image-processing and vision-based tasks, such as object tracking, image segmentation, and recognition. Their ability to adapt to changing data in real-time makes them particularly effective at handling tasks that involve complex patterns and temporal dynamics. For example, researchers at MIT have used LNNs to guide drones through previously unseen environments, and they have been found to perform better than other neural networks in navigational tasks.
- 3. Natural Language Understanding: LNNs are well-suited for natural language processing tasks, such as sentiment analysis and machine translation. Their ability to learn from real-time data allows them to adapt to changing language patterns and new phrases, making them more accurate at understanding the underlying emotion behind text. This is particularly useful in applications such as sentiment analysis, where the ability to accurately understand the emotional tone of text is important.
Constraints & Challenges of Liquid Neural Networks
Liquid Neural Networks (LNNs) are a type of neural network that have shown great promise in various applications, including time series data processing and forecasting, image and video processing, and natural language understanding. However, like any other technology, LNNs also have some constraints and challenges that need to be addressed.
One of the main challenges faced by LNNs is the vanishing gradient problem, which occurs when the gradients used to update the weights of the neural network become extremely small. This issue prevents the network from reaching the optimum weights, and thus, limits its ability to learn long-term dependencies effectively.
Another challenge faced by LNNs is the parameter tuning issue. LNNs have multiple parameters, including the choice of ODE solver, regularization parameters, and network architecture, which must be adjusted to achieve the best performance. Finding suitable parameter settings often requires an iterative process, which can be time-consuming and costly. If the parameter tuning is not done efficiently or correctly, it can result in suboptimal network response and reduced performance.
Another issue faced by LNNs is the lack of literature on their implementation, application, and benefits. Limited research makes it challenging to understand the maximum potential and limitations of LNNs. They are less widely recognized than other neural network architectures such as CNNs, RNNs, or transformer architecture.
Despite these challenges, researchers are still experimenting with the potential use cases of LNNs. They have the potential to be more dynamic, adaptive, efficient, and robust than traditional neural networks. As the technology continues to evolve, it is likely that the challenges faced by LNNs will be addressed, and their full potential will be realized.
Implementation of Liquid Neural Network in Pytorch
Training a Liquid Neural Network (LNN) in PyTorch involves several steps, including defining the network architecture, implementing the ODE solver, and optimizing the network parameters. Here's a step-by-step guide to training an LNN in PyTorch:
1. Install PyTorch:
pip install torch
2. Import necessary libraries:
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np3. Define the network architecture:
LNNs consist of a series of layers, each of which applies a nonlinear transformation to the input. The output of each layer is passed through a leaky ReLU activation function, which helps to introduce nonlinearity in the network.
import torch.nn as nn class LiquidNeuralNetwork(nn.Module): def __init__(self, input_size, hidden_size, num_layers): super(LiquidNeuralNetwork, self).__init__() self.hidden_size = hidden_size self.num_layers = num_layers self.layers = nn.ModuleList([self._create_layer(input_size, hidden_size) for _ in range(num_layers)]) def _create_layer(self, input_size, hidden_size): return nn.Sequential( nn.Linear(input_size, hidden_size), nn.LeakyReLU(), nn.Linear(hidden_size, hidden_size) ) def forward(self, x): for i, layer in enumerate(self.layers): x = layer(x) return x
4. Implement the ODE solver:
The ODE solver is responsible for updating the weights of the network based on the input data. You can use PyTorch's autograd system to implement the ODE solver.
import torch import torch.nn as nn class ODESolver(nn.Module): def __init__(self, model, dt): super(ODESolver, self).__init__() self.model = model self.dt = dt def forward(self, x): with torch.enable_grad(): outputs = [] for i, layer in enumerate(self.model.layers): outputs.append(layer(x)) x = outputs[-1] return x def loss(self, x, t): with torch.enable_grad(): outputs = [] for i, layer in enumerate(self.model.layers): outputs.append(layer(x)) x = outputs[-1] return x
5. Define the training loop:
The training loop updates the weights of the network based on the input data and the ODE solver.
def train(model, dataset, optimizer, epochs, batch_size): model.train() total_loss = 0 for epoch in range(epochs): for batch in dataset: inputs, labels = batch optimizer.zero_grad() outputs = model(inputs) loss = model.loss(inputs, outputs) loss.backward() optimizer.step() total_loss += loss.item() print(f'Epoch {epoch+1}, Loss: {total_loss / len(dataset)}')


its very helpful and interesting blog post and keep sharing articles like this informative content best erp for manufacturing industries in chennai
ReplyDelete