Sorting algorithms are essential tools in computer science and data processing. They allow us to organize and arrange data in a specific order, making it easier to search, analyze, and manipulate. One important aspect of sorting algorithms is their stability, which refers to the preservation of the relative order of equal elements during the sorting process. In this article, we will explore a new stable sorting algorithm called Quadsort, which belongs to the merge sort family and offers improved performance compared to other popular sorting algorithms
1. Stable Sorting
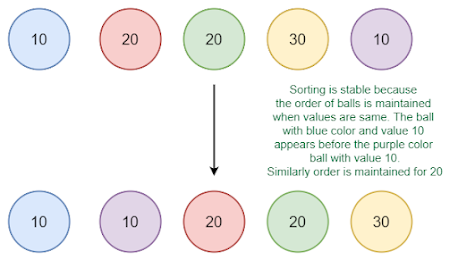
Stable sorting algorithms are particularly useful when sorting data that contains multiple elements with the same key value. In such cases, a stable sorting algorithm will preserve the original order of these elements, ensuring that they appear in the same order in the sorted output as they did in the input. This property is crucial for many applications, such as sorting a list of people by their last names and then by their first names.
Overview of Quadsort
Quadsort is a stable, non-recursive, adaptive merge sort that offers several advantages over other sorting algorithms, such as quicksort. It achieves its efficiency through a two-stage process and the use of quadruple exchanges, which allow for faster comparisons and swaps
2. The main steps of the Quadsort algorithm are as follows:
- Analyzer: The algorithm examines the array in groups of eight elements. It performs four comparisons on elements (1,2), (3,4), (5,6), and (7,8), storing the results and creating a bitmask with a value between 0 and 15 for all possible combinations. A bitmask value of 0 indicates that all four comparisons were in order.
- Quadruple Exchange: Quadsort is based on a quadruple exchange, which allows for efficient swapping of elements. This operation is performed on groups of four elements, ensuring that the relative order of equal elements is preserved.
- Rotations: By using rotations, the swap space of Quadsort is further reduced from n/2 to n/4. Rotations can be performed with minimal performance loss by using monobound binary searches and trinity/bridge rotations.
- Merge: Finally, the algorithm merges the sorted subarrays to produce the final sorted output.
Example of Quadsort
To better understand the Quadsort algorithm, let's consider an example with the following unsorted array:
[5][2][3][1][6][4][5][2][3][1][6][4]
1. Analyzer: The algorithm examines the array in groups of eight elements. In this case, the first group is [5][2][3][1][6][4][5][2][3][1][6][4]. It performs four comparisons: (5, 2), (8, 3), (1, 6), and (4, 7). The results are stored, and a bitmask is created with a value of 0, indicating that all four comparisons were in order.
2. Quadruple Exchange: The algorithm performs a quadruple exchange on the first group, resulting in the sorted group [2][3][5][1][4][6][2][3][5][1][4][6]. The relative order of equal elements (5 and 8) is preserved.
3. Rotations: The algorithm performs rotations on the second group [1][4][6][1][4][6], reducing the swap space from n/2 to n/4.
4. Merge: Finally, the algorithm merges the two sorted subarrays [2][3][5][2][3][5] and [1][4][6][1][4][6] to produce the final sorted output [1][2][3][4][5][6][1][2][3][4][5][6].
Implementation Steps and Complexity
The following pseudocode outlines the possible implementation steps for the Quadsort algorithm:
quadsort(array, left, right)
if (right - left) <= 1
return
mid = (left + right) / 2
quadsort(array, left, mid)
quadsort(array, mid, right)
merge(array, left, mid, right)The complexity of the Quadsort algorithm can be analyzed as follows:
- Time Complexity: Quadsort has a worst-case time complexity of O(nlogn), where n is the number of elements in the input array. This is the same as other efficient sorting algorithms, such as merge sort and quicksort.
- Space Complexity: Quadsort has a space complexity of O(n), which means it requires additional memory to store the input array and the temporary arrays used during the sorting process.
In conclusion, Quadsort is a new stable sorting algorithm that offers improved performance compared to other popular sorting algorithms. Its two-stage process, use of quadruple exchanges, and efficient rotations make it a valuable tool for sorting large datasets. By understanding the principles and steps of Quadsort, developers can choose the most appropriate sorting algorithm for their specific needs and optimize their applications for better performance and efficiency.

Comments
Post a Comment