SwiGLU (Swish-Gated Linear Unit) is a novel activation function that combines the advantages of the Swish activation function and the Gated Linear Unit (GLU). This activation function was proposed in a paper by researchers at the University of Copenhagen in 2019, and has since gained popularity in the deep learning community.
In this blog post, we will explore the SwiGLU activation function in detail and discuss its advantages over other activation functions.
What is an Activation Function?
In neural networks, activation functions are used to introduce non-linearity into the output of a neuron. They are responsible for deciding whether or not a neuron should be activated, based on the input it receives.
Activation functions help neural networks to learn complex non-linear relationships between inputs and outputs. There are several types of activation functions used in deep learning, such as the 'sigmoid', 'ReLU', and 'tanh'.
What is Swish Activation Function?
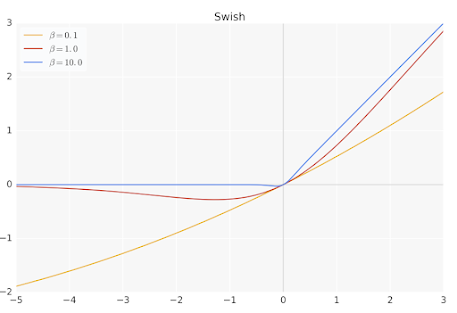
Swish is a non-monotonic activation function that was proposed by Google researchers in 2017. Swish is defined as follows:
Swish(x) = x * sigmoid(beta * x)where 'beta' is a trainable parameter.
Swish has been shown to perform better than ReLU in many applications, especially in deep networks. The main advantage of Swish is that it is smoother than ReLU, which can lead to better optimization and faster convergence.
What is GLU Activation Function?
Gated Linear Units (GLU) are a type of activation function that were proposed by researchers at Microsoft in 2016. GLU is defined as follows:
GLU(x) = x * sigmoid(Wx + b)
where 'W' and 'b' are trainable parameters.
GLU is similar to Swish in that it combines a linear function with a non-linear function. However, in GLU, the linear function is gated by a sigmoid activation function.
GLU has been shown to be particularly effective in natural language processing tasks, such as language modeling and machine translation.
What is SwiGLU Activation Function?
SwiGLU is a combination of Swish and GLU activation functions. SwiGLU is defined as follows:
SwiGLU(x) = x * sigmoid(beta * x) + (1 - sigmoid(beta * x)) * (Wx + b)
where 'W', 'b', and 'beta' are trainable parameters.
In SwiGLU, the Swish function is used to gate the linear function of GLU. This allows SwiGLU to capture the advantages of both Swish and GLU, while overcoming their respective disadvantages.
SwiGLU has been shown to outperform both Swish and GLU in a variety of tasks, including image classification, language modeling, and machine translation.
Advantages of SwiGLU Activation Function
The main advantages of SwiGLU over other activation functions are:
- Smoothness: SwiGLU is smoother than ReLU, which can lead to better optimization and faster convergence.
- Non-monotonicity: SwiGLU is non-monotonic, which allows it to capture complex non-linear relationships between inputs and outputs.
- Gating: SwiGLU uses a gating mechanism, which allows it to selectively activate neurons based on the input it receives. This can help to reduce overfitting and improve generalization.
- Performance: SwiGLU has been shown to outperform other activation functions, including Swish and GLU, in a variety of tasks.
SwiGLU Implementation in TensorFlow
Here is a simple function of SwiGLU in TensorFlow. The function is found in a GitHub Repository of ActTensor:
class SwiGLU(tf.keras.layers.Layer):
def __init__(self, bias=True, dim=-1, **kwargs):
"""
SwiGLU Activation Layer
"""
super(SwiGLU, self).__init__(**kwargs)
self.bias = bias
self.dim = dim
self.dense = tf.keras.layers.Dense(2, use_bias=bias)
def call(self, x):
out, gate = tf.split(x, num_split=2, axis=self.dim)
gate = tf.keras.activations.swish(gate)
x = tf.multiply(out, gate)
return xSummary
SwiGLU is a novel activation function that combines the advantages of Swish and GLU activation functions. This post was just a simple introduction to the SwiGLU activation function and its advantages in the field.

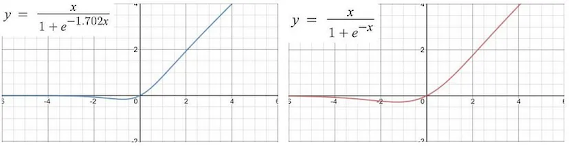
Comments
Post a Comment