Artificial intelligence has revolutionized how we interact with the world, from personal assistants to self-driving cars. Deep neural networks, in particular, have driven much of this progress. However, these networks are typically large, complex, and computationally expensive. In some cases, it is not feasible to use these models in real-world applications, especially when deploying to low-powered devices. To solve this problem, researchers have developed a technique known as knowledge distillation, which allows us to compress large neural networks into smaller, faster, and more efficient ones.
In this blog post, we will explore the concept of knowledge distillation, its mathematical underpinnings, and its applications. Additionally, we will provide an implementation of knowledge distillation in Keras, one of the most popular deep-learning frameworks.
https://neptune.ai/blog/knowledge-distillation
What is Knowledge Distillation?
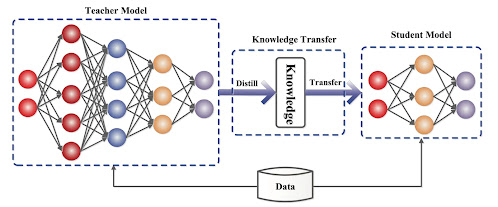
Knowledge distillation is a technique used to transfer knowledge from a large, complex model (known as the teacher model) to a smaller, simpler model (known as the student model). The goal of this transfer is to maintain the accuracy of the teacher model while reducing the computational cost of the student model.
The basic idea behind knowledge distillation is that the teacher model has learned a lot of valuable information during its training, which the student model can leverage. Specifically, we aim to transfer the "soft" labels generated by the teacher model to the student model, rather than the "hard" labels used during training.
Soft labels are probability distributions generated by the teacher model over the output space, whereas hard labels are binary values indicating the correct class. Soft labels provide more information than hard labels and capture the uncertainty of the teacher model's predictions. By training the student model to match the soft labels generated by the teacher model, we can create a smaller model that is better able to capture the complexity of the original model.
Mathematical Concepts
To understand how knowledge distillation works mathematically, we need to introduce some key concepts. Let's consider a neural network with input x, output y, and parameters $θ$, which we denote as $fθ(x) = y$
The softmax function is a popular choice for the output activation function in classification tasks. The softmax function maps the outputs of the final layer of a neural network to a probability distribution over the output classes. Mathematically, the softmax function is defined as:
$softmax(z)i = ezi / ∑jezj$
where $zi$ is the ith output of the final layer and the sum is over all outputs of the final layer.
The temperature parameter T is a hyperparameter that controls the "softness" of the output probabilities. Higher values of T produce softer probabilities, while lower values produce harder probabilities. We can use the softmax function with a temperature parameter to obtain the soft labels generated by the teacher model. The softmax function with a temperature parameter is defined as:
$softmaxT(z)i = ezi/T / ∑jezj/T$
where T is the temperature parameter.
The cross-entropy loss is a popular choice for classification tasks. It measures the difference between the predicted probability distribution and the true probability distribution. The cross-entropy loss between the predicted distribution p and the true distribution q is defined as:
$CE(p,q) = - ∑iqilog(pi)$
where pi is the ith element of the predicted distribution p and qi is the ith element of the true distribution q.
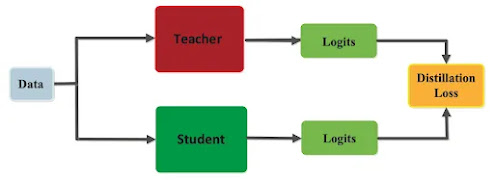
Now, let's consider a teacher model with parameters θT and a student model with parameters θS. We aim to train the student model to match the soft labels generated by the teacher model. Specifically, we want to minimize the following loss function:
$L = αT * CE(softmaxT(fθT(x)/T), softmaxT(fθS(x)/T)) + αH * CE(softmax(fθT(x/T), y)$
where $αT$ and $αH$ are hyperparameters that control the relative importance of the two terms, $softmaxT(fθT(x)/T)$ is the soft label generated by the teacher model, $softmaxT(fθS(x)/T)$ is the soft label predicted by the student model, $softmax(fθT(x))$ is the hard label generated by the teacher model, y is the true label, and CE is the cross-entropy loss.
The first term in the loss function encourages the student model to match the soft labels generated by the teacher model, while the second term encourages the student model to match the hard labels used during training. The temperature parameter T controls the "softness" of the output probabilities, and the hyperparameters $αT$ and $αH$ control the relative importance of the two terms.
Applications of Knowledge Distillation
Knowledge distillation has several applications in deep learning. Here are a few examples:
Model Compression: Knowledge distillation can be used to compress large, complex models into smaller, simpler models. This allows us to deploy models to low-powered devices that would not be able to handle the larger models.
Ensemble Methods: Ensemble methods involve combining multiple models to improve performance. However, this comes at the cost of increased computational complexity. Knowledge distillation can be used to combine multiple models into a single, smaller model that maintains the accuracy of the original ensemble.
Transfer Learning: Transfer learning involves leveraging knowledge from pre-trained models to improve performance on new tasks. Knowledge distillation can be used to transfer knowledge from a pre-trained model to a smaller model, allowing us to fine-tune the smaller model on a new task more efficiently.
Implementation in Keras
Now that we understand the theory behind knowledge distillation, let's look at an implementation in Keras. We will use the CIFAR-10 dataset, which consists of 60,000 32x32 color images in 10 classes.
First, let's define the teacher model. We will use a pre-trained ResNet50 model as the teacher model:
from tensorflow.keras.applications.resnet50 import ResNet50
teacher_model = ResNet50(weights='imagenet', include_top=True)Next, let's define the student model. We will use a smaller ResNet18 model as the student model. Then, let's define the loss function. We will use the loss function described earlier, with αT=0.5 and αH=0.5:
from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, Dropout, Flatten from tensorflow.keras.applications.resnet50 import ResNet50 def build_student_model(input_shape, num_classes): model = Sequential() model.add(ResNet18(include_top=False, weights=None, input_shape=input_shape)) model.add(Flatten()) model.add(Dense(512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(num_classes, activation='softmax')) return model student_model = build_student_model(input_shape=(32, 32, 3), num_classes=10)
import tensorflow.keras.backend as K
def distillation_loss(y_true, y_pred, teacher_pred, temperature=5):
alpha = 0.5
T = temperature
soft_loss = alpha * K.mean(K.categorical_crossentropy(K.softmax(teacher_pred / T), K.softmax(y_pred / T)))
hard_loss = (1 - alpha) * K.mean(K.categorical_crossentropy(y_true, y_pred))
return soft_loss + hard_lossWe can then compile and train the student model using the distillation loss:
from tensorflow.keras.optimizers import Adam
optimizer =Adam(lr=0.001)
student_model.compile(loss=lambda y_true, y_pred: distillation_loss(y_true, y_pred, teacher_model.output),
optimizer=optimizer, metrics=['accuracy'])
student_model.fit(x_train, y_train, batch_size=64, epochs=10, validation_data=(x_test, y_test))After training the student model using the distillation loss, we can evaluate its performance on the test set and compare it to a student model trained using the standard cross-entropy loss.
# Evaluate student model on test set
test_loss, test_acc = student_model.evaluate(x_test, y_test)
# Print test set results
print('Test loss:', test_loss)
print('Test accuracy:', test_acc)
By comparing the test set accuracies of the two models, you can see which one performed better on the test set. If the student model trained with knowledge distillation has a higher accuracy, it means that it was able to learn from the teacher model and improve its performance compared to the student model trained with cross-entropy loss alone. Otherwise, if the student model trained with cross-entropy loss has a higher accuracy, it means that the standard training approach was more effective in this particular case.

Comments
Post a Comment